Extended Euclidian Algorithm Explained

In this blog post, I explain the Euclidian Algorithm (+extended) and how to implement them in python.

Prerequisite: Modulus Operator#

First, we need to understand the modulus operator.

The modulus operator, often represented by the percent character (%) in many programming languages, returns the rest of the division between 2 operands.

For example, let’s say we have 2 integers a=5 and b=2. Then a mod b will be equal to 1

~ ❯ python3
Python 3.13.7 (main, Aug 14 2025, 00:00:00) [GCC 14.3.1 20250523 (Red Hat 14.3.1-1)] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> a=5
>>> b=2
>>> a%b
1

We can also think of it as:

How much would remain if we put the maximum possible number of bs inside a ?

In our example, q=2 is the maximum number of times we can fit b into a without going over. And the remainder (to reach the value of a) is r=1. This can be seen in the below figure:

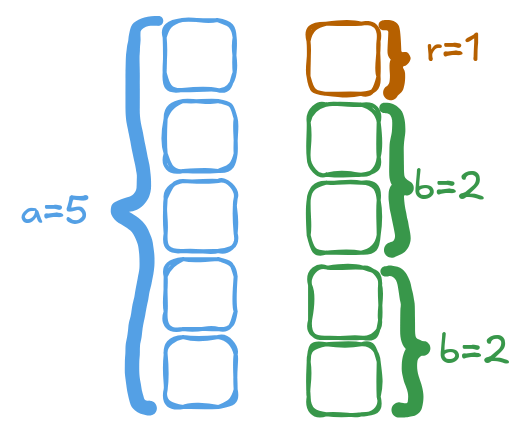
Euclidian Algorithm#

The Euclidian algorithm is used to get the Greatest Common Divisor d of 2 integers a and b (ie. the biggest number that divides both a and b).

In order to find the gcd, the algorithm relies on the following claim:

if a and b are both divisible by d, then r = a mod b is also divisible by d

but how can we prove it ?

Approach 1: math

What we know: both a and b are divisible by d.

What we are trying to prove: r = a mod b is also divisible by d.

$$ x = ny $$

where n is also an integer.

Knowing this, a and b could be written:

Using this and the earlier formula (a=bq+r) we get:

r can be written as an integer (n-mq) times d, therefore r is divisible by d.

Approach 2: visual intuition

In this approach, we need to think of x being divisible by y as x being made of n blocks of size y (x, y, n integers).

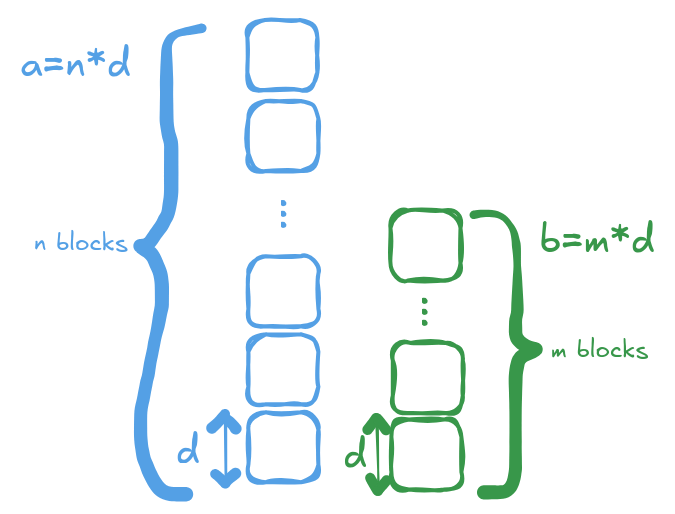
In the above figure, we see that a is made of n blocks of size d and b is made of m blocks of size d. This is the same as a=n*d and b=m*d

In this illustration, we can see that the remainder r will always be made up of a whole number of blocks of size d, thus will always be divisible by d. This is because r is what remains when you substract b “q times” from a (ie. r = a - bq) and since a and b are made of the same unit blocks, naturally the remainder will also be the same.

Now coming back to the Euclidian Algorithm.

We have shown that if a and b are divisible by d, then r = a mod b is also divisible by d.

And we know that a and b are both divisible by gcd(a,b), which means that r = a mod b is also divisible by gcd(a,b).

So r, being smaller than a and b, will naturally have the same gcd as them.

We can therefore write:

This helps a lot in reducing the possibilities, since finding the gcd for smaller numbers is easier that larger ones.

Implementation#

The algorithm will first compute r = a % b.

If r is equal to 0, it will return min(a,b)

Else it will return gcd(min(a,b), r)

def gcd(a, b):
    r = a % b

    if r == 0:
        return min(a, b)

    return gcd(min(a, b), r)

print(gcd(12,44))

Extended Euclidian Algorithm#

The extended euclidan algorithm is a way to find 2 integers x and y such that:

To start, let’s look at the simplest case first: when r=0.

If we are given 2 integers a and b (a > b) and r = a % b = 0, then b (the smallest) is the gcd.

In this case, x would be 0 and y would be 1:

This will be the base case of the recursion.

Now let’s try to understand the different steps involved.

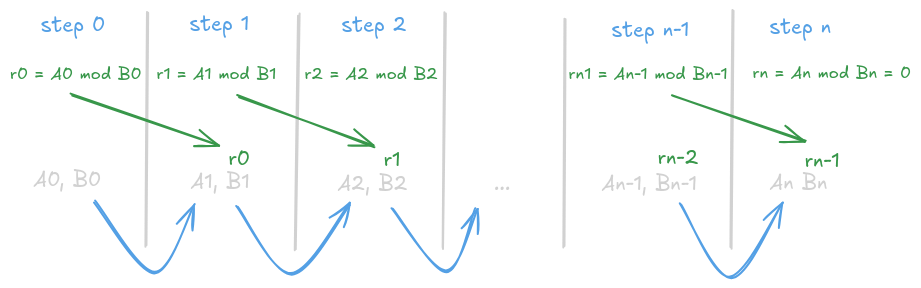
At the start, we are given 2 integers A0 and B0 (A0 > B0) and we are trying to find:

• d = gcd(A0, B0)
• x and y such that $$x*A0+y*B0=d$$

At step 0, we compute r0 = A0 % B0, if it’s not 0 we move to step 1 with A1 = B0 and B1 = r0.

At step 1, we repeat the same until we reach step n.

At step n, we compute rn = An % Bn and find that it is equal to 0. We have reached the base case, so we return d=Bn, x=0, y=1:

Then, we go back to step n-1. Here we need to recalculate x and y for An-1 and Bn-1, because the previous values we had were for An and Bn. For each step we need to have right values of x and y, until we ultimately get back to step 0 where we’ll have the final values.

We can generalize this problem in the following manner:

Knowing the values x and y for step k, what are the values for step k-1 ?

From the arrows in the illustration, we can see:

• Ak = Bk-1
• Bk = rk-1 = Ak-1 - Bk-1 * qk-1

Knowing this, we can find the new values of x and y:

In the end we have:

Implementation#

We now have everything we need to implement the algorithm.

def f(a, b):
    # Calculating the remainder
    r = a % b

    # Base case
    if r == 0:
        arr = [b, 0, 1]
        return arr

    else:
        arr = f(b, r)

        # Calculating the new values of x and y
        new_x = arr[2]
        new_y = arr[1] - arr[2] * (a//b)

        arr = [arr[0], new_x, new_y]
        return arr


a = 12
b = 44
res = f(a, b)
print(f"{res[0]} = {res[1]} * {a} + {res[2]} * {b}")